The Field Equations of Gravitation By A. Einstein
I have shown in two recently published reports, how one can arrive at field equations of gravitation, that are in agreement with the postulate of general relativity,
i.e. which in their general form are covariant in respect to arbitrary substitutions of space-time variables.
The line of development was as follows. At first I found equations, that contain
Newton's theory as approximation and that are covariant in respect to arbitrary substitutions of the determinant 1. Afterwards I found, that those equations in general correspond to covariant ones, if the scalar of the energy tensor of "matter" vanishes. The coordinate system had to be specialized in accordance with the simple rule, that

is made to 1, whereby the equations of the theory experience an eminent simplification. In the course of this, however, one had to introduce the hypothesis, that the scalar of the energy tensor of matter vanishes.
Recently I find now, that one is able to dispense with hypothesis concerning the energy tensor of matter, if one fills in the energy tensor of matter into the field equations in a somehow different way than it was done in my two earlier reports. The field equations for vacuum, upon which I based the explanation of the perihelion motion of mercury, remain untouched by this modification. I give the complete consideration again at this place, so that the reader is not forced to uninterruptedly consultate the earlier reports.
From the well known
Riemannian covariant of fourth rank, the following covariant of second rank is derived:
 | (1) |
 | (1a) |
 | (1b) |
[ 845 ] We obtain the ten general covariant equations of the gravitational field in spaces, in which "matter" is absent, by putting
 | (2) |
These equations can be formed in a simpler way, when one choses the reference system so that

. Then
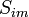
vanishes due to (1b), so that one obtains instead of (2)
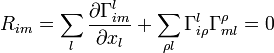 | (3) |
 | (3a) |
Here we put
 | (4) |
which magnitudes we will denote as the "components" of the gravitational field.
If "matter" exists in the considered space, then its energy tensor appears on the right hand side of (2) or (3). We put
 | (2a) |
where we put
 | (5) |

is the scalar of the energy tensor of "matter", the right hand side of (2a) is a tensor. If we specialize the coordinate system in the ordinary way again, then we obtain instead of (2a) the equivalent equations
 | (6) |
 | (3a) |
Like always we assume, that the divergence of the energy tensor of matter vanishes in the sense of the general differential calculus (Momentum-Energy theorem). When specializing the coordinate choice in accordance with (3a), it follows from it, that the

shall fulfill the conditions
 | (7) |
or
 | (7a) |
[ 846 ] If one multiplies (6) by

and sums over

and

, then one obtains in respect to (7) and in respect to the relation following from (3a)

the conservation law for matter and the gravitational field together in the form
 | (8) |
where

(the "energy tensor" of the gravitational field) is given by
 | (8a) |
The reasons that drove me to the introduction of the second member on the right-hand side of (2a) and (6), become clear from the following considerations, that are completely analogous to those given at the place just mentioned (p. 785).
If we multiply (6) by

and sum over the indices

and

, then we obtain after simple calculation
 | (9) |
where corresponding to (5) it is put for abbreviation
 | (8b) |
Note, that it follows from the additional term, that in (9) the energy tensor of the gravitational field occurs besides that of matter in the same way, which is not the case in equations (21)
l.c..
Furthermore one derives instead of equation (22)
l.c., in the way as it is given there by the aid of the energy equation, the relations:
![\frac{\partial}{\partial x_{\mu}}\left[\sum\limits _{\alpha\beta}\frac{\partial^{2}g^{\alpha\beta}}{\partial x_{\alpha}\partial x_{\beta}}-\varkappa(T+t)\right]=0](http://upload.wikimedia.org/wikisource/en/math/f/6/1/f615a0467d4efac9406038508f17001d.png) | (10) |
From our additional term it follows, that these equations contain no new condition in respect to (9), so that concerning the energy tensor
[ 847 ] of matter, no other presupposition has to be made than the one, that it has to be in agreement with the momentum-energy theorem.
By that, the general theory of relativity as a logical building is eventually finished. The relativity postulate in its general form that makes the space-time coordinates to physically meaningless parameters, is directed with stringent necessity to a very specific theory of gravitation that explains the perihelion motion of mercury. However, the general relativity postulate offers nothing new about the essence of the other natural processes, which wasn't already taught by the special theory of relativity. My opinion regarding this issue, recently expressed at this place, was erroneous. Any physical theory equivalent to the special theory of relativity, can be included in the general theory of relativity by means of the absolute differential calculus, without that the latter gives any criterion for the admissibility of that theory.
 is made to 1, whereby the equations of the theory experience an eminent simplification. In the course of this, however, one had to introduce the hypothesis, that the scalar of the energy tensor of matter vanishes.
is made to 1, whereby the equations of the theory experience an eminent simplification. In the course of this, however, one had to introduce the hypothesis, that the scalar of the energy tensor of matter vanishes.



 . Then
. Then 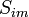 vanishes due to (1b), so that one obtains instead of (2)
vanishes due to (1b), so that one obtains instead of (2)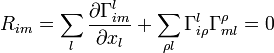




 is the scalar of the energy tensor of "matter", the right hand side of (2a) is a tensor. If we specialize the coordinate system in the ordinary way again, then we obtain instead of (2a) the equivalent equations
is the scalar of the energy tensor of "matter", the right hand side of (2a) is a tensor. If we specialize the coordinate system in the ordinary way again, then we obtain instead of (2a) the equivalent equations

 shall fulfill the conditions
shall fulfill the conditions

 and sums over
and sums over  and
and  , then one obtains in respect to (7) and in respect to the relation following from (3a)
, then one obtains in respect to (7) and in respect to the relation following from (3a)

 (the "energy tensor" of the gravitational field) is given by
(the "energy tensor" of the gravitational field) is given by
 and sum over the indices
and sum over the indices  and
and  , then we obtain after simple calculation
, then we obtain after simple calculation

![\frac{\partial}{\partial x_{\mu}}\left[\sum\limits _{\alpha\beta}\frac{\partial^{2}g^{\alpha\beta}}{\partial x_{\alpha}\partial x_{\beta}}-\varkappa(T+t)\right]=0](http://upload.wikimedia.org/wikisource/en/math/f/6/1/f615a0467d4efac9406038508f17001d.png)